The resource is a high-quality PDF document containing 12 separate questions.
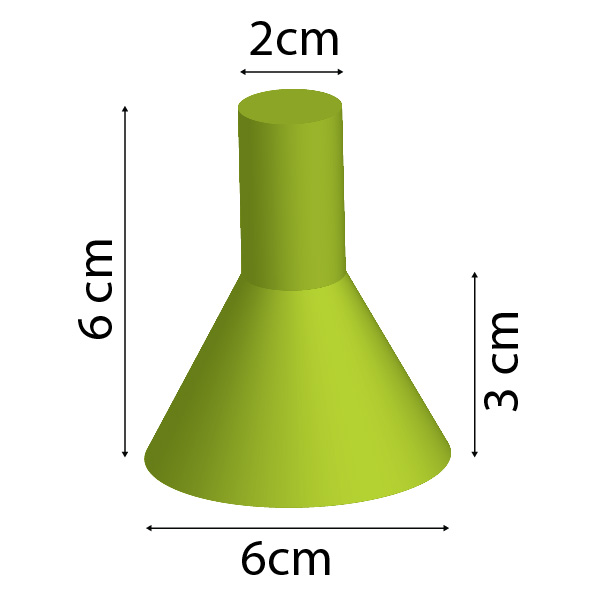
Volumes of Compound Shapes Worksheet
$1.00
Students will need to know how to calculate the volume of cuboids, spheres, and cylinders in order to complete all questions.
Each question contains an image of a compound shape for which students are required to calculate the volume.
Calculating the volume of compound shapes requires multiple skills. I strongly recommend that you spend time teaching/learning the basic volume formulae before attempting the questions on this worksheet.
The correct presentation of the method is key to successfully answering questions like these. Showing all steps and quoting each formula used will help to embed the processes.
How to Calculate the Volumes of Compound Shapes
To calculate the volumes of compound shapes you need to identify the shapes you are dealing with. For example, consider the shape in the image above; it is comprised of a triangular prism and a rectangular prism.
Separately calculate the volume of the rectangular prism and the volume of the triangular prism. Then add these two volumes together to calculate the total volume.
Remember to include the correct units with your answers. In the example above the units would be cm cubed.
For the volume of the triangular prism we have:
\begin{aligned}V & =\frac{8 \times 5}{2} \times 8 \\\\& =\frac{40}{2} \times 8 \\\\& =20 \times 8 \\\\& =160 \mathrm{~cm}^{3}\end{aligned}
For the volume of the rectangular prism we have:
\begin{aligned}V & =8 \times 15 \times 2 \\\\& =120 \times 2 \\\\& =240 \mathrm{~cm}^{3}\end{aligned}
Therefore the total volume is:
\begin{aligned}\text { Total Volume } & =\text { Triangular Prism }+\text { Rectangular Prism } \\\\& =160 \mathrm{~cm}^{3}+240 \mathrm{~cm}^{3} \\\\& =\underline{\underline{400 \mathrm{~cm}^{3}}}\end{aligned}
Request a Custom Worksheet Design
Let me know what you require using the form below and I will be in touch.