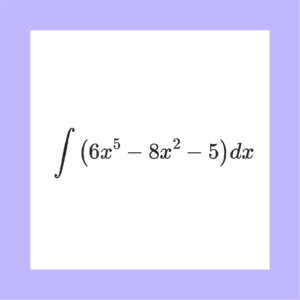When answering the integration worksheets questions, students will need to consider the simplification of fractional coefficients.
Here is an example of one of the questions together with my full solution:
$$
\begin{aligned}
& \int\left(8 x^3-4 x+5\right) d x \\\\
= & \frac{8}{4}x^4-\frac{4}{2}x^2+5 x+c \\\\
= & 2 x^4-2 x^2+5 x+c
\end{aligned}
$$
Here is a second example. This time there are fractions in the answer.
$$
\begin{aligned}
& \int\left(4 x^5+6 x^3-4\right) d x \\\\
= & \frac{4}{6}x^6+\frac{6}{4}x^4-4 x+c \\\\
= & \frac{2}{3}x^6+\frac{3}{2} x^4-4 x+c
\end{aligned}
$$
Buy the Integration Worksheets
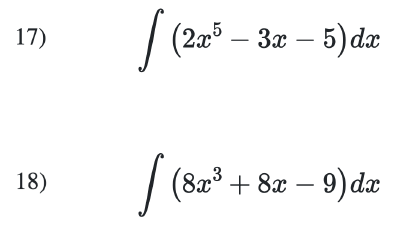
Integration Worksheets 100 Questions and Answers
$1.00
Tutoring Request
Are there any complex integration problems?
There are many challenging integration problems, and the level of difficulty can depend on the background and knowledge of the person attempting the problem. Here are a few examples of integration problems that may be considered difficult:
Improper integrals: These are integrals where the function being integrated is infinite or discontinuous over the range of integration. These types of integrals can be difficult to evaluate because standard techniques may not work.
Integrals involving special functions: Special functions are mathematical functions that have specific properties and occur frequently in mathematics and physics. Examples include the gamma function and the Bessel functions. These types of integrals can be challenging to evaluate due to the complexity of the functions involved.
Multivariate integrals: These are integrals that involve more than one variable, and they can be difficult to evaluate because of the added complexity.
Integration by parts: This is a method for evaluating certain types of integrals by breaking them up into the product of two simpler functions. While this method can be very useful, it can also be challenging to apply because it requires careful algebraic manipulation.